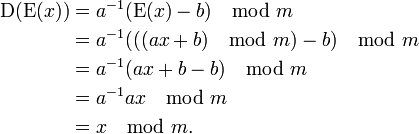Affine Cipher in Python
Affine Cipher
A simple mono alphabetic substitution cipher I used to help me level up my programming/math skills :) Though I would not suggest using it for anything other than education/historic purposes since it is highly insecure (by means of frequency analysis, brute force, guessing or otherwise).From Wikipedia
In the affine cipher the letters of an alphabet of size m are first mapped to the integers in the range 0..m − 1. It then uses modular arithmetic to transform the integer that each plaintext letter corresponds to into another integer that correspond to a ciphertext letter. The encryption function for a single letter is
where modulus m is the size of the alphabet and a and b are the key of the cipher. The value a must be chosen such that a and m are coprime. The decryption function is
where a − 1 is the modular multiplicative inverse of a modulo m. I.e., it satisfies the equation
The multiplicative inverse of a only exists if a and m are coprime. Hence without the restriction on a decryption might not be possible. It can be shown as follows that decryption function is the inverse of the encryption function
Python Code
Download: Affine_Encrypt_Decrypt.py
#Encryption Function
#E(x) = eaffine = (ax + b) mod m
def eaffine(a, b):
print "This is the encrypted Alphabet\n (plain text : cipher text)\n" #sets the mod to 26
for i in range(26):
#Prints the plain text alphabet and it's corresponding ciphertext alphabet values
#Note: ascii A is 65, so we have to add/sub 65 to account for ascii value (so that A is essentialy set to 0)
print chr(i+65) + ": " + chr(((a*i+b)%26)+65)
print "Now that we have the transposition table, let's encrypt a plaintext message\n"
#User inputs the plain text message they want encrypted
plaintext = raw_input("Message (in capitals):")
# Start with and empty list for the encrypted message
ciphertext = []
#Finds the numerical value for each letter in the plain text and puts it in the list
for x in plaintext:
ciphertext.append(ord(x))
#Append the corresponding plain text character to encrypted one
for i in range(len(ciphertext)):
#encryption algorithm
ciphertext[i] = chr(((a*(ciphertext[i]-65)+b)%26)+65)
#Print the original and the encrypted message
print plaintext + ": " + " ".join(ciphertext)
#Decryption Function
#D(x) = daffine = ainverse *(x-b) mod m
def daffine(a, b):
print "This is the decrypted Alphabet\n (cipher text : plain text)"
#sets the mod to 26
for i in range(26):
#Finds the modular multiplicative inverse of a, which is needed in the function below for decrypting
ainverse = a**(phi(a)-1)%26
#Prints the cipher text alphabet and it's corresponding plain text alphabet values
print chr(i+65) + ": " + chr((ainverse*(i- b))%26+65)
print "Now that we have the transposition table, let's decipher that message\n"
#User inputs the ciphertext they want decrypted
ciphertext =raw_input("Enter encrypted message (in capitals): ")
# Start with and empty list to store the decrypted message
plaintext = []
#Finds the numerical value for letter in the ciphertext and puts it in the list
for x in ciphertext:
plaintext.append(ord(x))
#Append the corresponding ciphertext character to plain text
for i in range(len(plaintext)):
#decryption algorithm
plaintext[i] = chr((ainverse*((plaintext[i]-65)- b))%26+65)
#Print the cipher text and the decrypted message
print ciphertext + ": " + " ".join(plaintext) + '\n'
#Other Functions Needed for Decryption
#Greatest common divisor
def gcd(a,b):
#Return the gcd of two positive integers.
while b != 0:
a, b = b, a%b
print a
print b
return a
#Coprime
def coprime(a,b):
#return True if 'a' and 'b' are coprime.
return gcd(a,b) == 1
#Euler's Totient Function
def phi(m):
if m == 1:
return 1
else:
r = [n for n in range(1,int(m)) if coprime(int(m),int(n))]
#Returns the number/length of coprime numbers that make up m
return len(r)
print "Would you like to encrypt (enter e) or decrypt (enter d) the message? "
decision = raw_input("> ")
if decision == "e":
print "Enter the key: "
a = int(input("a key: "))
b = int(input("b key: "))
eaffine(a, b)
elif decision == "d":
print "Now that you have a secret message let's decipher it!"
print "Enter the key: "
a = int(input("a key: "))
b = int(input("b key: "))
daffine(a, b)
else:
print "I hope you liked the program!"
Some Keys of Interest
Atbash Affine Cipher: a= 25, b =25Ciphertext example: ZGYZHSXRKSVI
Caesar cipher: a= 1, b =3
Ciphertext example: FDHVDUFLSKHU
ROT13: a=1, b=13
Ciphertext example: EBGPVCURE
Notes
The code is only set to work with plain text that is all in capitals. It doesn’t handle spaces or punctuation very well either, so that I’ll leave to someone else to improve on (or maybe my future self :P)The “a” value for the key must be coprime with m, in this case m = 26 (i.e., if gcd(a, m) = 1; the number 26 has 12 numbers that it’s coprime with [1,3,5,7,9,11,15,17,19,21,23,25]).
References
Other Affine Ciphers
Affine cipher. (2011, June 14). In Wikipedia, The Free Encyclopedia. Retrieved 19:17, August 12, 2011, from < link >
Atbash. (2011, July 12). In Wikipedia, The Free Encyclopedia. Retrieved 18:24, August 12, 2011, from < link >
Caesar cipher. (2011, June 11). In Wikipedia, The Free Encyclopedia. Retrieved 19:05, August 12, 2011, from < link >
Classical cipher. (2011, May 3). In Wikipedia, The Free Encyclopedia. Retrieved 19:52, August 12, 2011, from < link >
ROT13. (2011, August 11). In Wikipedia, The Free Encyclopedia. Retrieved 19:05, August 12, 2011, from < link >
Math Used
Euclidean algorithm. (2011, August 11). In Wikipedia, The Free Encyclopedia. Retrieved 19:28, August 12, 2011, from <link>
Euler’s totient function. (2011, August 7). In Wikipedia, The Free Encyclopedia. Retrieved 18:32, August 12, 2011, from <link>
Kozdron, Michael. “Affine Ciphers, Decimation Ciphers, and Modular Arithmetic.” Math 135: Affine Ciphers. Cornell University, June-July 2006. Web. 10 Aug. 2011. <link>.
Modular arithmetic. (2011, July 26). In Wikipedia, The Free Encyclopedia. Retrieved 21:47, August 12, 2011, from <link>.
Modular multiplicative inverse. (2011, July 10). In Wikipedia, The Free Encyclopedia. Retrieved 19:13, August 12, 2011, from <link>.
“99 Prolog Problems Solutions” Wiki Python. Web. 10 Aug. 2011. <link>.